Викторина «Числовые следы или Балахнинские прогрессии». Нулевой (пробный) тур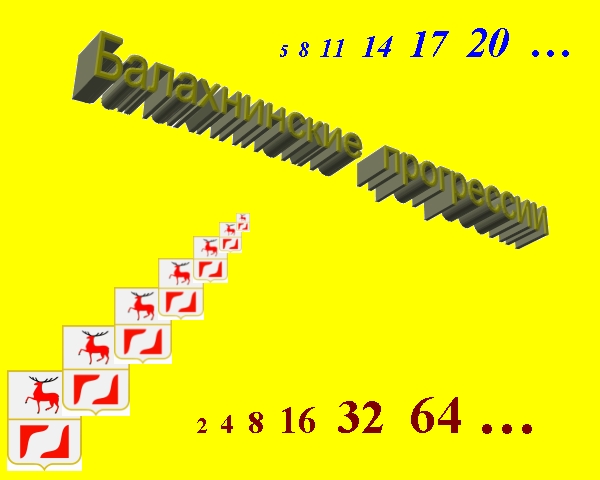

Итак, друзья, мы начинаем нашу викторину. В новом конкурсе – прежняя основа: требуется знание родного города. А вот конкретика теперь отличается от того, что было у нас раньше. Придется вспомнить школьную математику. Не бойтесь, уважаемые земляки! Ничего сложного!

Прогрессии – что это такое и какие они бывают?
Начнем с арифметической прогрессии. Вот простейший пример: 3, 5, 7, 9, … Каждое следующее число в этой цепочке отличается от предыдущего на одну и ту же величину, здесь - на два.

Еще один пример: 120, 99, 78, 57, 36, … Здесь числа расположены по убыванию, и разность между соседними числами – 21.
Постоянная величина, на которую отличаются соседние числа в последовательности, называется РАЗНОСТЬЮ арифметической прогрессии.

А теперь геометрическая прогрессия. Типичный пример: 2, 6, 18, 54, … Здесь очередное число последовательности получается из предыдущего умножением на константу. В этом примере эта константа равна трем. Такое число называется ЗНАМЕНАТЕЛЕМ геометрической прогрессии.

Всё просто, не так ли, друзья?

В нашей викторине нас не будут интересовать такие тонкости, как убывание или возрастание. Главное – умение в куче чисел выделить несколько из них, которые образуют какую-нибудь конкретную прогрессию.

Важное замечание. Формально для арифметической прогрессии ее разность может быть равна нулю, т.е., к примеру, цепочка чисел 7, 7, 7, 7, … тоже является арифметической прогрессией. Кроме того, приведенную последовательность чисел можно считать и геометрической прогрессией со знаменателем, равным единице.
Так вот, друзья, такие СТАЦИОНАРНЫЕ прогрессии мы НЕ рассматриваем – мы их попросту игнорируем (даже если они случайно где-то промелькнут)!

Теперь ближе к сути конкурса. В каждом туре мы будем публиковать несколько пронумерованных (для удобства) фотоснимков родной Балахны. Это могут быть и старые, и современные фотографии. Для каждого фото нужно попытаться найти ПОДХОДЯЩЕЕ число. А затем, располагая набором из нескольких чисел (по количеству фотографий в данном туре), надо попытаться выделить из них как минимум (!) ЧЕТЫРЕ числа, образующие арифметическую или геометрическую прогрессию. Витиевато выражаясь, по имеющимся отпечаткам «числовых следов» надо обнаружить скрытую строгую закономерность. Это и будет решением загадки тура.

О каких числах, которые «привязываются» к конкретным объектам города, идет речь? Конечно же, о номерах строений (жилых домов или учреждений)! Именно о номерах строений (улица такая-то, дом номер…), а НЕ о номерах учреждений (типа «детсад №30»)! Номера с буквами (№1Б, №2А и т.п.) игнорируем: это вообще НЕ числа!
Вроде бы всё просто? Нет, дорогие земляки, у нас будут маленькие хитрости.

Во-первых, в каждом туре, за исключением пробного, всегда будет не менее ШЕСТИ фотографий – и среди них одна, две (или даже больше) обязательно будут «ложными». Т.е. в конкретном туре среди предложенных N фото некоторые снимки будут введены в исходный набор исключительно для того, чтобы запутать игроков. Другими словами, скрытая прогрессия будет состоять из меньшего, чем N, количества фотографий (но, как было уже подчеркнуто, не меньше четырех). Правильное решение – это всегда максимально длинная цепочка, т.е. если, к примеру, игрок нашел прогрессию из четырех чисел, а на самом деле она длиннее, то это лишь ЧАСТИЧНО верное решение.

Во-вторых, в кадре может оказаться не одно, а несколько строений – все их надо учитывать. Но и это еще не всё! В непосредственной близости от точки съемки (гораздо ближе, чем до самого объекта, который мы видим на снимке, - например, всего в нескольких метрах от фотографа) – сзади, слева или справа - тоже могут быть строения (дома). И их номера тоже следует включать в анализ!
В некоторых (впрочем, нечастых) случаях исходное фото может быть специально «подрезано» так, что на снимке вообще не видно ни одного здания.

Подразумевается, что где-то рядом с левым или правым срезом кадра расположено что-то существенное.
Что же у нас получается? А вот что. Каждому снимку может соответствовать от одного до нескольких чисел. Таким образом, в попытке нащупать скрытую прогрессию придется повозиться с различными вариантами (комбинациями) чисел из нескольких имеющихся групп!

Рассмотрим пример. Допустим, в очередном туре игрокам предъявлены ШЕСТЬ фотографий. Для каждой фотографии надо понять, что конкретно мы тут видим, т.е. надо найти соответствующий уголок нашего города и сообразить, где стоял фотограф, что оказалось у него слева (справа, сзади).

Вот игрок отыскал объекты города для всех шести фото. К примеру, у него получилось следующее:
снимок №1: видны дома 45 и 47 (на какой-то улице), за спиной фотографа (совсем рядом) – строение 20 (это другая улица, поскольку тут рядом перекресток), т.е. отобраны числа 20, 45 и 47;
снимок №2: отобраны числа 60 и 61;
снимок №3: отобраны числа 1, 2 и 15;
снимок №4: отобраны числа 98 и 99;
снимок №5: отобраны числа 21, 22 и 30;
снимок №6: только одно число – 32.

Придется пораскинуть мозгами, пытаясь выделить прогрессию, которая состоит минимум их четырех чисел.
Вот берем: от снимка №3 – число 15, от снимка №5 – число 30, а от снимка №2 – число 60. Получаем последовательность 15, 30, 60 – в ней каждое последующее число получается из предыдущего умножением на ДВА: геометрическая прогрессия. Увы, в этой цепочке всего три числа – мало! (Вот если для какого-то другого из оставшихся снимков мы имели бы число 120, вот тогда получили бы «полноценную» прогрессию вида 15, 30, 60, 120.)

Всматриваемся, комбинируем, думаем и, наконец, находим решение задачи: 15, 30, 45, 60 – арифметическая прогрессия с разностью 15. Каждое из этих четырех чисел «привязано» к СВОЕМУ снимку, при этом фотографии №4 и №6 оказались ложными следами.

Еще раз подчеркнем: одна фотография – одно число в искомой последовательности! Нельзя брать два (или более) числа от одного и того же фото!

Примечание. Почти все объекты, которые использованы в нашем конкурсе, найти будет не так уж и сложно. Почему? Потому что никаких глухих улочек и переулков теперь не будет: все строения либо находятся рядом с оживленными автотрассами, либо расположены от них не так уж и далеко (не более 200 метров). Но будут и приметные дома вдали от главных улиц: это старые характерные постройки или «модерн».

Всего в нашем соревновании будет 12 (двенадцать) зачетных туров. Итоги мы поведем в самом начале марта будущего года.

Ну, что ж, уважаемые земляки, вот пять снимков нулевого (пробного) тура:












Как обычно, результаты пробного тура в зачет не пойдут, но зато наши игроки почувствуют, что такое поиск числовых следов. Будьте внимательны, друзья: уже в нулевом туре присутствует маленькая хитрость!
Небольшую подсказку мы все-таки дадим: когда фотограф делал одну из фотографий, он едва не коснулся спиной какой-то стены…

Как оформлять свой ответ? Конечно, желательно подробнее – чтобы не возникало никаких вопросов к игроку. Например, так:

снимок №3 – число 2 (номер дома слева от фотографа – этот дом на улице «AAA» оказался за пределами кадра);
снимок №4 – число 4 (улица «BBB»: в правой части кадра – строение с таким номером);
снимок №1 – число 8 (видна улица «CCC» с несколькими строениями, но прямо за спиной фотографа, приблизительно в пяти метрах – дом №8 по улице «DDD»);
снимок №5 – число 16 (дом по центру кадра на улице «EEE»);
снимок №2 – это ложный след (числа 33, 34 – в кадре дома по улице «FFF»).
Решение: геометрическая прогрессия 2, 4, 8, 16.

Внимание, уважаемые участники! Теперь время приема решений ограничиваем моментом 20.30 (двадцать часов тридцать минут)! Просьба не опаздывать!
Итак, свой ответ надо прислать до 20.30 8-го декабря (понедельник) по нашему традиционному электронному адресу ba-rebus@yandex.ru.

Приступайте к поискам, друзья!